Técnicas de IA para Biologia
5 - Autoencoders
André Lamúrias
Autoencoders
Summary
- What are Autoencoders?
- Different restrictions on encoding
- Undercompleteness
- Regularization
- Sparsity
- Noise reconstruction
- Applications
Autoencoders
What are autoencoders?
What are autoencoders?
Network trained to output the input (unsupervised)
- In the hidden layers, one layer learns a code describing the input

Cat images: Joaquim Alves Gaspar CC-SA
What are autoencoders?
Network trained to output the input (unsupervised)
- The encoder maps from input to latent space

Cat images: Joaquim Alves Gaspar CC-SA
What are autoencoders?
Network trained to output the input (unsupervised)
- The decoder maps from latent space back to input space

Cat images: Joaquim Alves Gaspar CC-SA
What are autoencoders?
Network trained to output the input (unsupervised)
- Encoder, $h = f(x)$, and decoder, $x = g(h)$
- No need for labels, since the target is the input
- Why learn $x = g\left(f\left(x\right)\right)$?

Cat images: Joaquim Alves Gaspar CC-SA
What are autoencoders?
Network trained to output the input (unsupervised)
- Encoder, $h = f(x)$, and decoder, $x = g(h)$
- Why learn $x = g\left(f\left(x\right)\right)$?
- Latent representation can have advantages
- Lower dimension
- Capture structure in the data
- Data generation
What are autoencoders?
Network trained to output the input (unsupervised)
- Encoder, $h = f(x)$, and decoder, $x = g(h)$
- Autoencoders are (usually) feedfoward networks
- Can be trained with the same algorithms, such as backpropagation
- But since the target is $x$, they are unsupervised learners
- Need some "bottleneck" to force a useful representation
- Otherwise just copies values
Autoencoders
Different types of autoencoders
Undercomplete Autoencoders
Autoencoder is undercomplete if $h$ is smaller than $x$
- Forces the network to learn reduced representation of input
- Trained by minimizing a loss function $$L(x,g(f(x)))$$ that penalizes the difference between $x$ and $g(f(x))$
- If linear it is similar to PCA (without orthogonality constraint)
- With nonlinear transformations, an undercomplete autoencoder can learn more powerful representations
- However, we cannot overdo it
- With too much power, autoencoder can just index each training example and learn nothing useful: $$f(x_i) = i,\quad g(i) = x_i$$
Undercomplete Autoencoders
Autoencoder is undercomplete if $h$ is smaller than $x$
- Mitchell's autoencoder, hidden layer of 3 neurons

Manifold Learning
Manifold
- A set of points such that the neighbourhood of each is homeomorphic to a euclidean space
- Example: the surface of a sphere

Manifold Learning
- Data may cover a lower dimension manifold of the space
Manifold Learning
- Learn lower dimension embeddings of data manifold
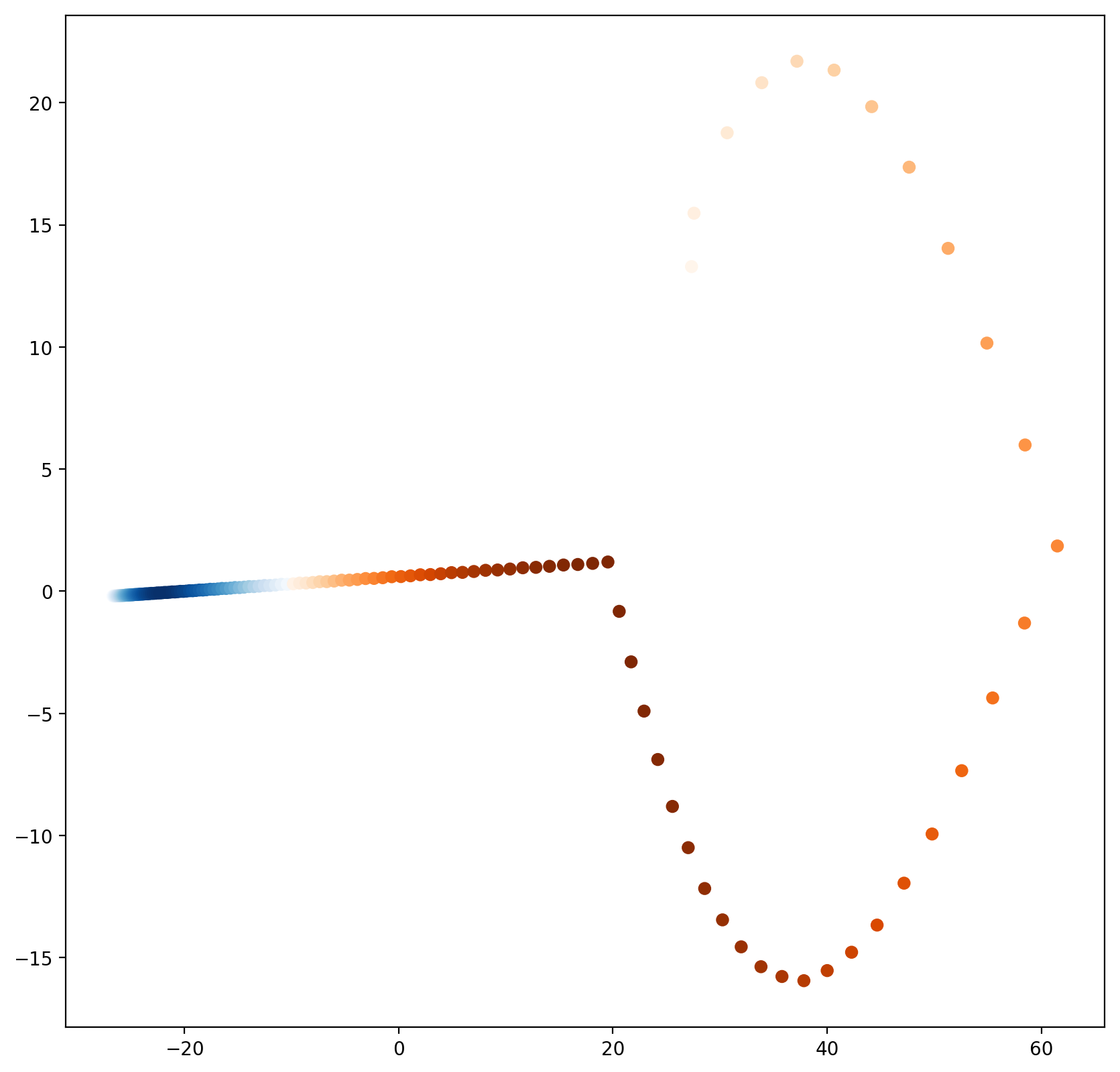

Undercomplete Autoencoders
- Nonlinearity makes dimensionality reduction adapt to manifold
- PCA vs autoencoder 6,4,2,4,6, UCI banknote dataset (4 features)
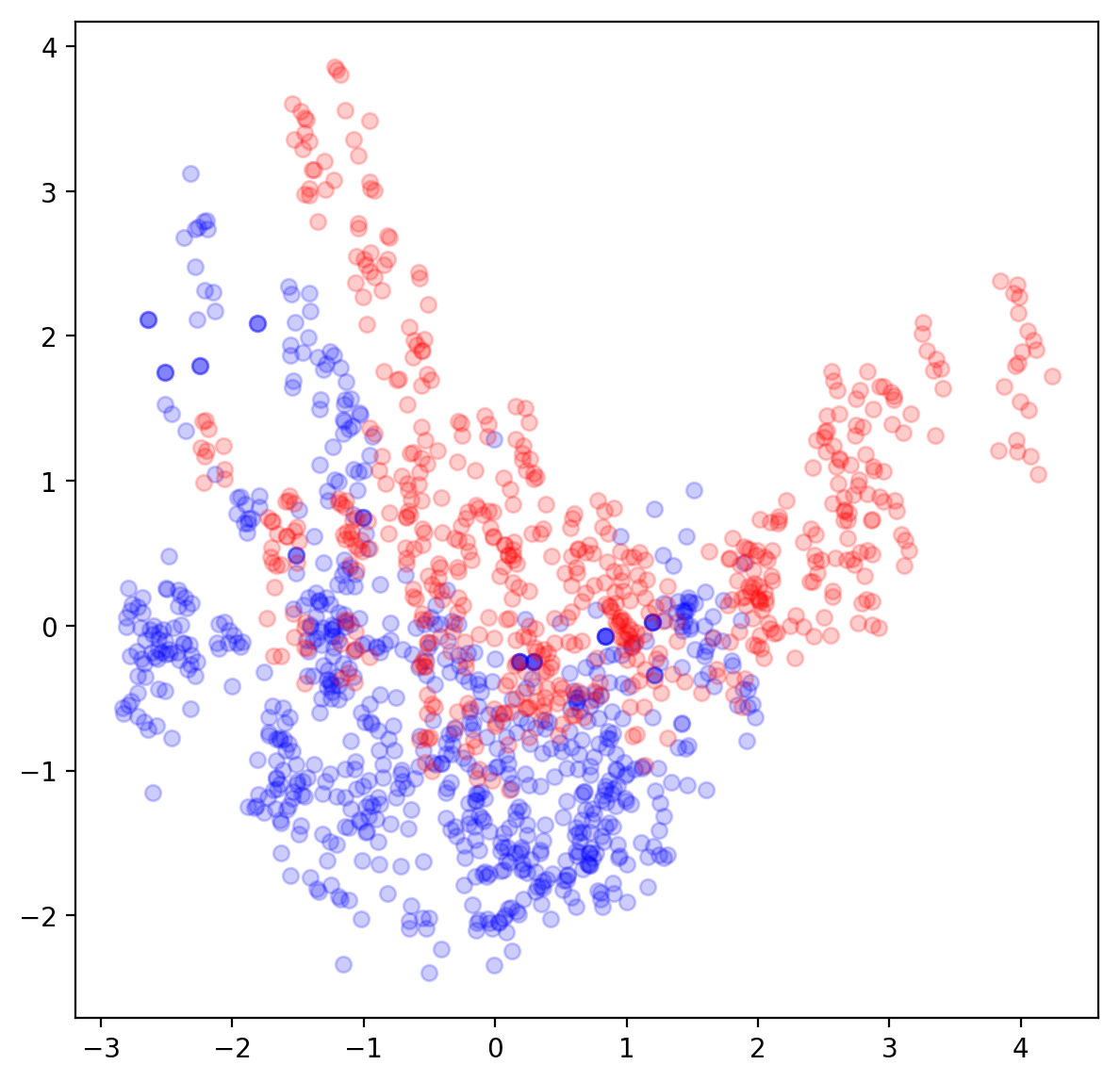

Manifold Learning
Manifold learning with autoencoders
- This works because we force the network in two opposite ways:
- We demand the ability to reconstruct the input
- But we also constrain how the network can encode the examples
- Undercompleteness is just one way of doing this
Beware of overfitting.
- If the autoencoder is sufficiently powerful, it can reconstruct the training data accurately but lose generalization power
- In the extreme, all information about reconstructing the training set may be in the weights and the latent representation becomes useless
Regularized Autoencoders
An overcomplete autoencoder has $h$ larger than $x$
- This, by itself, is a bad idea as $h$ will not represent anything useful

Cat images: Joaquim Alves Gaspar CC-SA
Regularized Autoencoders
An overcomplete autoencoder has $h$ larger than $x$
- But we can restrict $h$ with regularization
- This way the autoencoder also learns how restricted $h$ should be
Regularized Autoencoders
Sparse Autoencoder
- Force $h$ to have few activations
- Example: we want the probability of $h_i$ firing $$\hat p_i = \frac{1}{m} \sum_{j=1}^m h_i(x_j)$$ to be equal to $p$ (the sparseness parameter)
Regularized Autoencoders
Sparse Autoencoder
- Include in the loss function a penalization term
- Use the Kullback-Leibler divergence between Bernoulli variables as a regularization penalty $$L(x,g(f(x)))+\lambda \sum_i\left( p \log \frac{p}{\hat p_i} +(1-p) \log \frac{1-p}{1-\hat p_i}\right)$$
- Other options include L1 regularization applied to the activation of the neurons, L2, etc.
Regularized Autoencoders
Sparse Autoencoder
- Sparse autoencoders make neurons specialize

Image: Andrew Ng
- Trained on 10x10 images
- 100 neurons on $h$
- Images (norm-bounded) that maximize activation
Regularized Autoencoders
Sparse Autoencoder
- Sparse autoencoders trained on MNIST, different sparsity penalties
- (25 neurons in filter, images correspond to highest activation)

Niang et. al, Empirical Analysis of Different Sparse Penalties... IJCNN 2015,
Regularized Autoencoders
Denoising Autoencoders
- We can force $h$ to be learned with noisy inputs
- Output the original $x$ from corrupted $\tilde x$: $L(x,g(f(\tilde x)))$
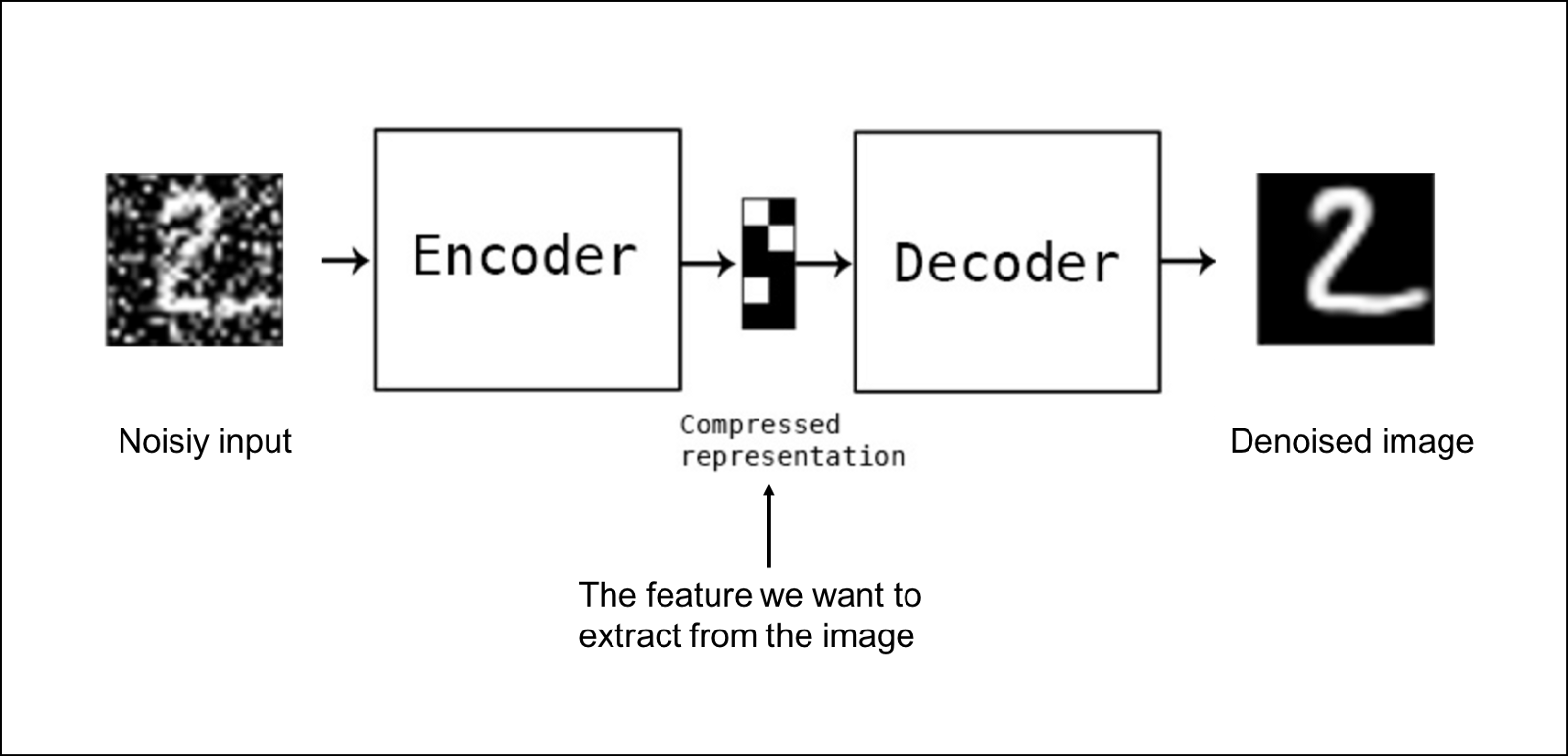
Image: Adil Baaj, Keras Tutorial on DAE
Regularized Autoencoders
Denoising Autoencoders
- We can force $h$ to be learned with noisy inputs
- Output the original $x$ from corrupted $\tilde x$: $L(x,g(f(\tilde x)))$
- This forces the autoencoder to remove the noise by learning the underlying distribution of $x$
- Algorithm:
- Sample $x_i$ from $\mathcal{X}$
- Apply corruption $C(\tilde{x_i}\ |\ x_i)$
- Train with $(x,\tilde x)$
Stochastic Autoencoders
- We can also use autoencoders to learn probabilities
- Just like with other ANN (e.g. softmax classifier)
- The decoder is modelling a conditional probability $p_{decoder}(x\ |\ h)$
- where $h$ is given by the encoder part of the autoencoder
- The decoder output units can be chosen as before:
- Linear for estimating the mean of Gaussian distributions
- Sigmoid for Bernoulli (binary)
- Softmax for discrete categories
- We can think of encoder and decoder as modelling conditional probabilities $$p_{encoder}(h\ |\ x) \qquad p_{decoder}(x\ |\ h)$$
Autoencoders
Generating Data
Generating Data
- Can we use autoencoders to generate new examples?

Cat images: Joaquim Alves Gaspar CC-SA
Generating Data
- Autoencoders create a latent representation from the data

Cat images: Joaquim Alves Gaspar CC-SA
Generating Data
- And then decode to recreate the data from this representation

Cat images: Joaquim Alves Gaspar CC-SA
Generating Data
- Can we use the decoder to generate new examples?
Discriminative vs Generative
- A discriminative model tries to approximate a function $p(y \mid x)$
- E.g. Logistic regression or softmax ANN predict the probability of each class given the features
- A generative model approximates $p(x,y)$ and then finds $p(y\mid x)$: $$p(x,y) = p(y\mid x)p(x) $$
- This is generative because, knowing $p(x,y)$, we can sample from the distribution
With autoencoders
- We decode from $h$, so we need to find its distribution in order to generate examples from $p(h,y) = p(y\mid h)p(h)$
Generating Data
- Intuition: we need to sample the right part of the latent space

Cat images: Joaquim Alves Gaspar CC-SA
Generating Data
- Intuition: if outside the right region, the result is garbage

Cat images: Joaquim Alves Gaspar CC-SA
Generating Data
Generative adversarial networks
- Fix the latent space with some distribution
- The result will be garbage because net not trained

Cat images: Joaquim Alves Gaspar CC-SA
Generating Data
Generative adversarial networks
- Train a network to distinguish the real examples from fakes

Generating Data
Generative adversarial networks
- One network creates examples from given distribution
- The other distinguishes real from fake
- Train both, alternating, so each becomes increasingly better

Ian Goodfellow
Generating Data
Generative adversarial networks
- One network creates examples from given distribution
- The other distinguishes real from fake
- Train both, alternating, so each becomes increasingly better
- As a result, the generator learns to map our fixed initial distribution to the space of our target examples.
Generating Data
- Can we use autoencoders to generate new examples?
- Yes, if we know the "shape" of the latent space
Variational Autoencoders
- Train the autoencoder to encode into a given distribution
- E.g. mixture of independent Gaussians
- This way we learn the distribution for generating examples of each type

Variational Autoencoders
- How do we backpropagate through random sampling?
- Reparametrize: $z$ is deterministic apart from a normally distributed error $$z = \mu + \sigma \odot \epsilon \qquad \epsilon \sim \mathcal{N}(0,1)$$

Image: Jeremy Jordan, Variational autoencoders.
Variational Autoencoders
- VAE can learn to disentangle meaningful attributes
- We can force the independence of the latent variables

Image: Bouchacourt et. al., Multi-level variational autoencoder, 2018
Autoencoders
Convolutional Autoencoders
Convolutional Autoencoders
Use convolutions and upsampling to reconstruct
- Latent space is narrow, need to restore original dimensions

Barna Pásztor, Aligning hand-written digits with Convolutional Autoencoders
Convolutional Autoencoders
- Upsample followed by convolution (in 2D)
from tensorflow.keras.layers import UpSampling1D,UpSampling2D
UpSampling1D(size=2)
UpSampling2D(size=(2, 2), data_format=None, interpolation='nearest')
![]()
Shi et. al., Is the deconvolution layer the same as a convolutional layer?
Applications
Example: deep fakes
- Train the same encoder on different sets of inputs
- But for each set reconstruct with a specific decoder
- With this we can "translate" between sets
Applications
Example: deep fakes

Gaurav Oberoi, Exploring DeepFakes, https://goberoi.com/exploring-deepfakes-20c9947c22d9
Applications
Example: deep fakes
- Train with images from videos
- Process video:
- Input Fallon to encoder
- Output Oliver using Oliver decoder

Gaurav Oberoi, Exploring DeepFakes, https://goberoi.com/exploring-deepfakes-20c9947c22d9
Applications
Example: Text-to-image
- Stable Diffusion, DALL-e

Amazon Machine Learning Blog, https://aws.amazon.com/blogs/machine-learning/create-high-quality-images-with-stable-diffusion-models-and-deploy-them-cost-efficiently-with-amazon-sagemaker/
Applications
Example: Text-to-image
- Based on U-Net model architecture: CNN for image segmentation

Edge AI and vision, https://www.edge-ai-vision.com/2023/01/from-dall%C2%B7e-to-stable-diffusion-how-do-text-to-image-generation-models-work/
Autoencoders
Summary
Autoencoders
Summary
- Autoencoders: learn the input in the output
- Unsupervised learning
- Using restrictions (dimension, regularization)
- Or reconstruction (from corrupted inputs)
- Convolutional Autoencoders
- Recent applications
Further reading:
- Goodfellow et.al, Deep learning, Chapter 14